En este
apartado veremos la importancia de dada una función f, encontrar una función F
cuya derivada sea f, es decir que deseamos buscar una función F cuya derivada
sea f F’(x)=f(x) para toda x en algún
intervalo.
Antiderivada
Se dice que una
función F es una antiderivada de una función f sobre algún intervalo I si F’(x)
= f(x) para toda x en I
Una
antiderivada de f(x)=2cos(2x) es F(x)=sen(2x) puesto que F’(x)=2cos(2x)
Algo importante que hay que mencionar es que una función siempre tiene más de una antiderivada, así en el ejemplo anterior F1(x)= sen(3x) + 5 igual es una antiderivada de f(x)=2cos(2x) puesto que F’1(x)=2cos(2x)
Algo importante que hay que mencionar es que una función siempre tiene más de una antiderivada, así en el ejemplo anterior F1(x)= sen(3x) + 5 igual es una antiderivada de f(x)=2cos(2x) puesto que F’1(x)=2cos(2x)
Cualquier
antiderivada de f debe ser de la forma G(x)= F(x) + C, es decir, dos
antiderivadas de la misma función pueden diferir a lo más en una constante. Por
tanto, es F(x) + C la antiderivada más general de f(x).
La notación
F(x) + C representa una familia de funciones; cada miembro tiene una derivada
igual a f(x).
La antiderivada
más general de f(x) = 2cos(2x) es la
familia F(x)= sen(2x) + c
Como se ve en
la gráfica de la antiderivada de f(x) = 2cos(2x) es una traslación de la
gráfica de sen(2x)
Noción de la
integral definida
Por
conveniencia, se introducirá la notación para una antiderivada de una función.
Si F’(x)=f(x) la antiderivada más general de f se representa por
El símbolo de
la integral (el que está antes de f(x)dx en la fórmula de arriba) fue
introducida por Leibniz y se denomina signo integral
La notación parecida a una "s" alargada en la imagen de arriba se denomina integral indefinida de f(x)
respecto a x. La función f(x) se denomina integrando. El proceso de encontrar
una antiderivada se denomina antidiferenciación o integración. El numero C se
denomina constante de integración.
La diferenciación y la integración son procesos inversos
Esta fórmula establece una antiderivada de la derivada de una función es esa función más una constante
La
derivada de una antiderivada de una función es esa función.
A
partir de lo anterior se concluye que siempre que se obtiene la derivada de una
función, al mismo tiempo se obtiene una fórmula de integración.
De esta manera
es posible construir una fórmula de integración a partir de cada fórmula de derivada
Otra
antiderivada de gran importancia es la siguiente
Ejemplo 1
Podemos subir a x como numerador y tenemos
Ejemplo 2
PROPIEDADES
DE LA INTEGRAL DEFINIDA
Estas
propiedades se concluyen de inmediato a partir de las propiedades de la
derivada. Por ejemplo, ii) es una consecuencia del hecho de que la derivada de
una suma es la suma de las derivadas.
No
hay razón para usar dos constantes de integración, puesto que C1 y C2 ya sea que
se sumen o se resten se ha sustituido por la simple constante C.
Una
integral indefinida de cualquier suma infinita de funciones la podemos obtener
al integrar cada término













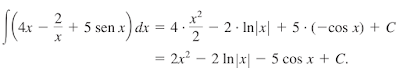
No hay comentarios:
Publicar un comentario